경제분석을 위한 역학모형

코로나 19의 충격과 그 여파로 전세계의 780억명의 개인은 사생활은 물론 경제활동에 심각한 영향을 받고 있다. 따라서 경제학자도 역학 조사와 그 연구 방법에 대해 상당한 관심을 쏟고 있는 상황이다. 특히 전통적인 역학 모형은 물론 다양한 진화된 방법론을 토대로 경제학적 모형을 개발하고 있다.

지금까지 가장 널리 알려진 역학 모형은 Kermack and McKendrick (1927)의 SIR 모형이다. 이 모형은 미분방정식을 바탕으로 한 동태 모형으로 모집단을 건강상태를 기준으로 세 가지 그룹( S : Susceptible, I : Infected, R : recovered )으로 분류하여 시간이 변함에 따라 그 흐름을 분석하는 방법이다.

경제학자는 올바른 개인의 의사 결정과 정부의 보건정책을 제안하기 위해, 전통적인 SIR 모형을 설명하는 미분방정식 위에 경제학적 조건식들을 추가하는 방법으로 모형을 개발한다.

1. 전통적인 SIR 모형 전통적인 모형에서는 다음과 같이 가정한다. 첫째, 모든 개인이 병에 걸릴 확률이 동일하고 병에 걸린 사람과의 접촉 수에 비례한다. 둘째, 병에 걸린 사람은 일정확률로 회복되며 한번 병에 걸린 뒤 회복되면 항체가 생겨 다시 그 병에 감염되지 않는다. 셋째, 전체 인구수는 일정하다. 이러한 조건을 바탕으로 모형화 하면 다음과 같은 조건을 얻을 수 있다.

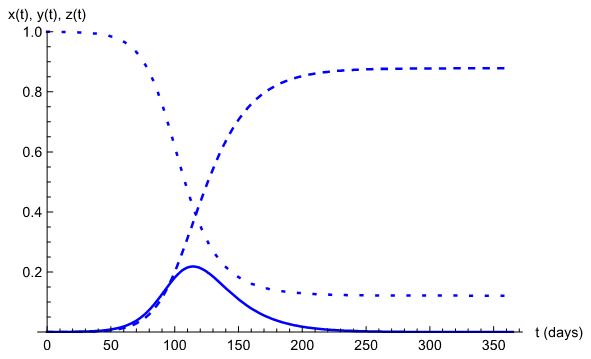
적절한 초기값을 바탕으로 미분방정식을 풀면 다음 그림과 같은 결과를 볼 수 있다. 감염되지 않은 수, S(t)는 아래 그림의 점선으로, 완치된 사람 수, R(t)는 끊어진 실선, 감염된 사람 수, I(t)는 실선으로 표시되어 있다.

2. 변형 SIR 모형

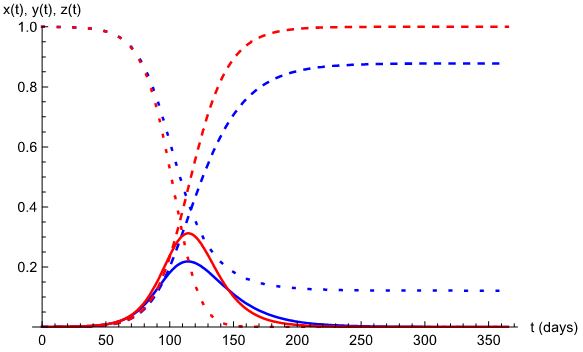
위에서 설명한 전형적인 SIR 모형의 감염에 대한 분석의 본질을 해치지 않으면서 경제정책적 부분을 첨가하기 위해 경제학자들이 변형 모형을 고안하고 있다. 전형적 모형에서 $\beta$와 $\gamma$를 외생변수 또는 상수로 취급했다면 이제는 정책에 따라서 바뀔 수 있는 부분으로 변형한 모형이다. 위의 전형적 모형과 같은 초기값으로 해를 구해 비교해 보면 다음 그림과 같아진다. 파랑색이 전통적인 모형, 빨강색이 변형 모형이다.

기초 감염 재생산 지수(R)

기초 감염 재생산 지수는 $\frac{\beta}{\gamma}$로 계산할 수 있는 한 명이 감염 되었을 때 그로 인해 발생하는 추가감염자수의 평균으로 해석할 수 있다. 감염자 수를 줄이기 위해서는 특히 재생산 지수를 낮추는 방법을 목표로 할 수 있는데, 따라서 $\beta$를 줄이거나 $\gamma$를 증가 시키는 것이다. 사회적 거리두기를 통한 감염자 와의 접촉확률을 줄이거나 벡신의 개발 등으로 $\beta$를 감소 시킬 수 있다. 각종 의료시설이나 치료재의 개발을 통한 $\gamma$의 증가 또한 재생산을 감소시키는 역할을 한다.

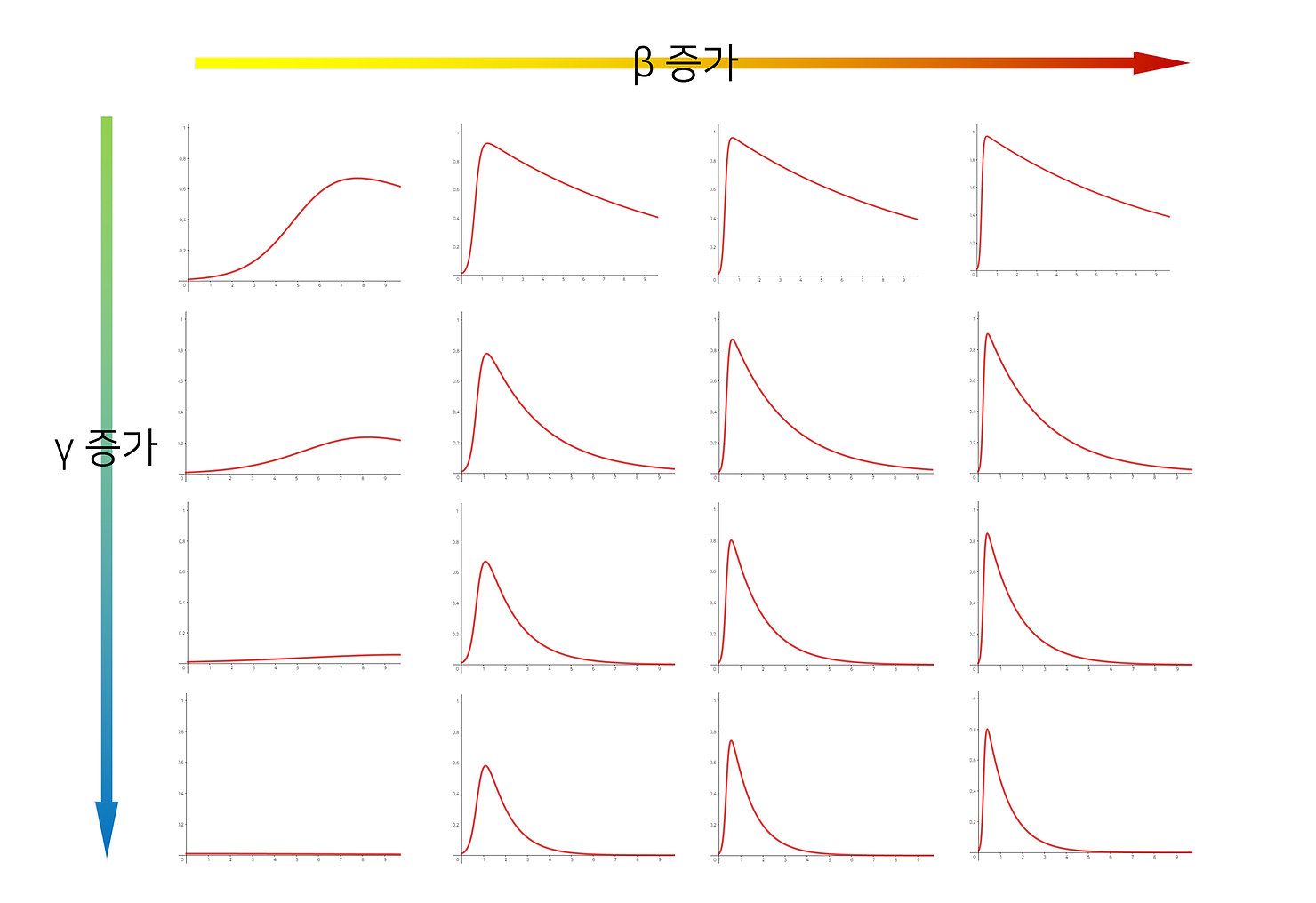
위 그림에서는 오른쪽으로 갈수록 또 위로 올라갈수록, 재생산 지수가 높아 지는 것을 의미하며, 감염자의 숫자가 폭발적으로 증가하고 그 수가 쉽게 감소하지 않는 상황을 잘 보여주고 있다.